| Темы | Предыдущий пункт | Следующая лекция | Литература | |
|
|
|

Первообразная функции. Неопределенный интеграл |
|
|
|
|
|
4.1.3. Интегралы, не выражающиеся через комбинацию элементарных функций |
|
При вычислении неопределенных интегралов возникает вопрос
Теорема Коши
Или другая формулировка.
Для каждой непрерывной в интервале (a, b) функции f(x)
существует функция F(x) , производная
от которой в интервале (a, b) в точности равна данной функции f(x).
Однако теорема Коши не утверждает, что первообразную данной функции
можно отыскать с помощью конечного числа известных операций и выразить
ответ в элементарных функциях. Основные способы вычисления интегралов в
элементарных функциях мы рассмотрим далее. Однако следует запомнить, что
некоторые интегралы нельзя найти таким образом. Их называют "неберущимися".
Под "неберущимися" интегралами подразумевают интегралы, которые не могут
быть выражены через конечное число арифметических операций и
суперпозиций элементарных функций. Например, доказано, что следующие интегралы не интегрируются
в элементарных функциях: Указанные интегралы хотя и существуют, но не являются элементарными функциями. Имеются другие способы для их вычисления. Например, с помощью разложения в бесконечный степенной ряд. Эти способы будут рассмотрены в одной из следующих лекций.
|
|
|
|
|
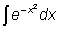 - интеграл Пуассона,
- интеграл Пуассона,
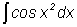 ,
,
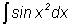 - интегралы Френеля,
- интегралы Френеля,
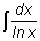 - интегральный логарифм,
- интегральный логарифм,
 - интегральный косинус,
- интегральный косинус,
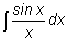 - интегральный синус.
- интегральный синус.