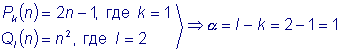| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Числовые ряды |
|
|
|
|
|
11.1.4 Исследование на сходимость рядов. Достаточные признаки сходимости.
|
||||
|
На практике обычно бывает трудно решить вопрос о сходимости данного ряда при помощи критерия Коши. Поэтому важно иметь такие достаточные признаки сходимости и расходимости, которыми было бы удобно пользоваться при исследовании рядов. Рассмотрим следующие достаточные признаки сходимости и расходимости рядов. Признак сравнения. Пусть имеем два ряда с положительными членами:
Если Доказательство: Пусть
ряд (2) сходится и сумма его равна V.
Тогда частичная сумма Пусть
теперь ряд (1) будет расходящимся.
Это означает, что его частичная сумма Для сравнения часто используются ряды:
Примеры Используя признак сравнения,
исследовать на сходимость следующие
ряды: 1) Решение:
Сравним данный ряд с
расходящимся, гармоническим рядом 2) Решение
Сравним данный ряд
с геометрической прогрессией т.е. сходящимся рядом, где
|
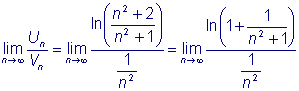
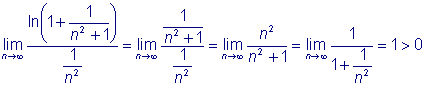 , но т.к. ряд (V) сходится, ряд (U)
тоже сходится.
, но т.к. ряд (V) сходится, ряд (U)
тоже сходится.