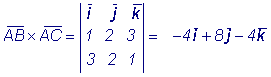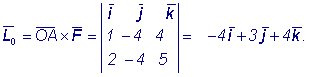| Темы | Предыдущий пункт | Следующий пункт | Литература | ||||||||
|
|
||||||||

Векторная алгебра |
||||||||
|
1.2.8 Векторное произведение. Как понятие скалярного произведения возникает из понятия работы, так понятие векторного произведения возникает из понятия момента силы.
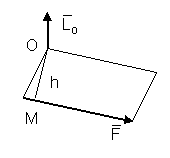
Пусть твердое тело
имеет одну неподвижную точку О. Пусть к точке М этого тела приложена сила
Момент силы
Определение. Векторным произведением двух векторов
1) имеет модуль, численно равный площади параллелограмма, построенного на перемножаемых векторах; 2) направлен перпендикулярно к перемножаемым векторам в ту сторону, откуда наименьший поворот первого множителя, совмещающий его направление с направлением второго множителя, виден происходящим против хода часовой стрелки. Обозначают векторное
произведение так:
где При равенстве нулю
векторного произведения:
Итак, векторное произведение двух векторов равно нулю тогда и только тогда, когда хотя бы один из перемножаемых векторов равен нулю или когда эти векторы коллинеарны. Имея в виду, что
нулевой вектор считается коллинеарным любому вектору, мы можем
сформулировать полученный результат короче: условием коллинеарности двух
векторов является равенство нулю их векторного произведения:
Законы векторного умножения 1) При перестановке множителей векторное произведение меняет только
свой знак:
2) Выполняется распределительный закон:
3) Выполняется закон сочетательности относительно скалярного
множителя:
Рассмотрим векторное произведение координатных ортов. В силу (*) имеем:
При рассмотрении
векторных произведений разноименных координатных ортов существенным
является предположение, что выбранная координатная система является
правой. При этом предположении вектор
то получаем
Для определения получающихся результатов удобно пользоваться схемой, приведенной на рис.2.17: Векторное произведение двух разноименных ортов, следующих друг за другом в направлении положительного обхода окружности, равно третьему орту со знаком плюс, в противоположном же случае - знаком минус. Используя это правило, получим следующую таблицу:
Векторное произведение в координатной форме Пусть два вектора
Перемножив почленно эти разложения, мы получим:
Отсюда, согласно правилам векторного перемножения ортов, будет следовать
или, после группировки коэффициентов у соответствующих ортов:
Полученные
коэффициенты при
Мы видим, что в
правой части получился развернутый определитель третьего порядка,
элементами первой строки которого являются векторы
Таким образом:
Это и есть окончательная формула, выражающая векторное произведение в координатной форме.
Пример 1. Найти векторное
произведение векторов
Решение: Имеем согласно формуле (2.8)
Пример 2. Вычислить площадь треугольника с вершинами
Решение: Находим векторы
Площадь
треугольника ABC равна
половине площади параллелограмма, построенного на векторах
Следовательно,
Ответ:
Пример 3. Упростить
выражение Решение: Используя законы векторного умножения, получим
Ответ:
Пример 4. Вычислить площадь
параллелограмма, построенного на векторах
Решение: Имеем
поскольку Итак, Ответ: 4 .
Пример 5. Сила
Решение: Искомый момент
обозначим
Ответ: |
|
|
|
|
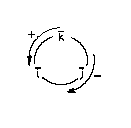
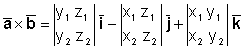 .
.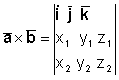
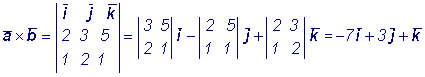 .
.