| Темы | Предыдущая лекция | Следующий пункт | Литература | |
|
|
|

Дифференциальные уравнения высших порядков |
|
|
|
|
Дифференциальное уравнение n -го порядка
имеет вид 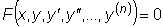 . .
В дальнейшем мы будем рассматривать уравнения, которые можно разрешить
относительно высшей производной. Пример
Рассмотрим дифференциальное уравнение
Найденное решение зависит от двух произвольных постоянных, при этом исходное дифференциальное уравнение было уравнением второго порядка. Такое решение называется общим решением этого уравнения.
Общим решением дифференциального уравнения n -го порядка
называется функция
Решения, получаемые из общего при закреплении постоянных
В прикладных вопросах часто приходится искать такое решение
дифференциального уравнения n-го порядка, которое удовлетворяет
n условиям:
Вообще говоря, последние условия, называемые начальными, выделяют из
общего решения
Задача отыскания решения дифференциального уравнения y (n) = f(x,y,y I,y II,..,y (n-1)) , удовлетворяющего n начальным условиям: y(xo ) = yo , y I (xo ) = y Io ,.., y (n-1) (xo ) = y (n-1)o называется задачей Коши.
|
|
|
|
|
|
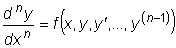 .
. 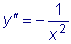 .
.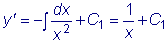 ,
, 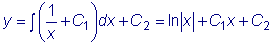 ,
, 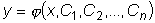 , существенно зависящая от
n произвольных постоянных и обращающая данное уравнение в
тождество при любых значениях этих постоянных.
, существенно зависящая от
n произвольных постоянных и обращающая данное уравнение в
тождество при любых значениях этих постоянных. 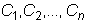 называются частными .
называются частными .
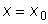 сама функция y и ее первые n -1 производных
сама функция y и ее первые n -1 производных 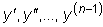
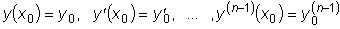 .
. 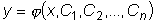 единственное частное решение.
единственное частное решение.