Этот метод используется, если функция справа имеет специальный вид:
f(x) = e ax [ Pm (x) cos(bx) + Qn (x) sin(bx) ], где
a и b - действительные числа,
Pm (x) и
Qn (x) - многочлены с действительными коеффициентами,
имеющими соответственно степени m >= 0 и n >= 0.
Вид частного решения неоднородного уравнения зависит от вида правой
части этого уравнения и подбирается в каждом случае с учетом корней
характеристического многочлена соответствующего однородного уравнения.
Можно показать, что частное решение имеет вид
y*(x) = xh e ax [ Ps (x) cos(bx) + Qs (x) sin(bx) ],
где a и b - те же числа, что и присутствующие в функции f(x),
h >= 0 - кратность корня (a + bi) для характеристичекого
многочлена соответствующего однородного уравнения, s = Max(m;n) ,
Ps (x) и Qs (x) - многочлены степени
s, подлежащие численному определению.
Рассмотрим некоторые частные случаи.
а) 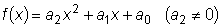 . .
Если
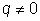 , то частное решение
неоднородного уравнения ищем также в форме квадратного трехчлена: , то частное решение
неоднородного уравнения ищем также в форме квадратного трехчлена:
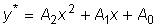 , ,
где
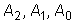 - неопределенные
коэффициенты. - неопределенные
коэффициенты.
Отсюда
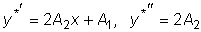 . .
Подставляя эти выражения
в исходное уравнение, мы получим тождество
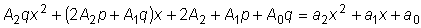 , ,
откуда
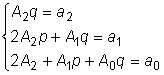 . .
Так как 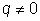 , то из последней системы
для коэффициентов , то из последней системы
для коэффициентов
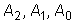 получаются определенные
числовые значения. Тем самым частное решение
y* будет вполне определено. получаются определенные
числовые значения. Тем самым частное решение
y* будет вполне определено.
Если 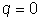 , то частное
решение y* ищем в виде , то частное
решение y* ищем в виде
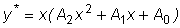 , когда один из корней
характеристического уравнения равен нулю, и в виде , когда один из корней
характеристического уравнения равен нулю, и в виде
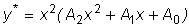 , ,
когда оба корня
характеристического уравнения нули. Аналогично обстоит дело, если
f(x) - многочлен P(x) произвольной степени.

Пример
Решить уравнение
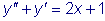 . .
Имеем:
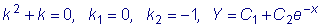 . .
Так как p=0, то частное решение данного уравнения ищем в виде
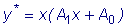 . .
Отсюда имеем:
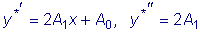 . .
Подставляем в исходное
уравнение: 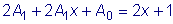 . .
Искомые
коэффициенты будут: 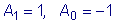 .
Значит, частное решение будет .
Значит, частное решение будет
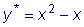 , ,
а общее решение
получается в виде
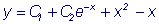 . .

б) 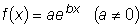 . .
Частное решение ищем в виде
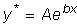 , ,
где A -
неопределенный коэффициент.
Отсюда
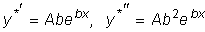 . .
Подставляя эти выражения в исходное уравнение, после сокращения на
e bx будем иметь
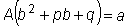 . .
Отсюда видно, что если
b не является корнем характеристического уравнения, то
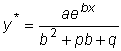 . .
Если b - корень характеристического уравнения, то
частное решение ищем в виде
y* = Axebx ,
когда b - однократный корень, и в виде
y* = P(x) ebx , когда b -
двукратный корень.
Аналогично будет, если
f(x) = P(x) ebx , где P(x) -
многочлен.

Пример
Решить уравнение
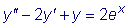 . .
Имеем:
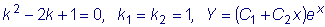 . .
Так как в данном
уравнении b = 1 - корень кратности два характеристического
уравнения, то частное решение данного уравнения ищем в виде
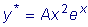 . .
Далее имеем:
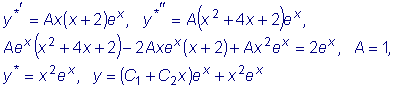 . .

в) 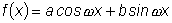 . (a и
b не нули одновременно). . (a и
b не нули одновременно).
В этом случае частное решение y*
ищем также в форме тригонометрического двучлена
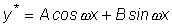 , ,
где A и
B - неопределенные коэффициенты.
Отсюда
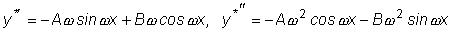 . .
Подставляя эти выражения в исходное уравнение, получим:
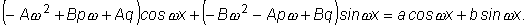 . .
Так как последнее равенство представляет собой тождество, то
коэффициенты при
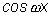 и и
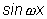 в левой и правой частях
этого равенства должны быть соответственно равны друг другу.
Поэтому в левой и правой частях
этого равенства должны быть соответственно равны друг другу.
Поэтому
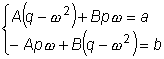 . .
Эти уравнения определяют коэффициенты A и B ,
кроме случая, когда
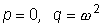
(или когда
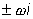 - корни характеристического
уравнения). - корни характеристического
уравнения).
В последнем случае частное решение исходного уравнения ищем
в виде
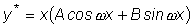 . .

Пример
Решить уравнение
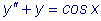 . .
Имеем:
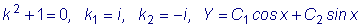 . .
Так как 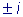 - корни
характеристического уравнения, то частное решение данного уравнения ищем
в виде - корни
характеристического уравнения, то частное решение данного уравнения ищем
в виде
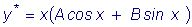 . .
Далее имеем:
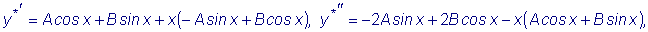
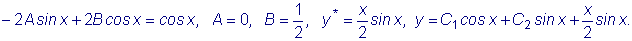 . .
|

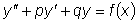 , где
p и q - действительные числа.
, где
p и q - действительные числа. 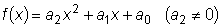 .
.
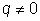 , то частное решение
неоднородного уравнения ищем также в форме квадратного трехчлена:
, то частное решение
неоднородного уравнения ищем также в форме квадратного трехчлена: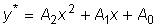 ,
,
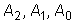 - неопределенные
коэффициенты.
- неопределенные
коэффициенты.
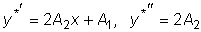 .
.
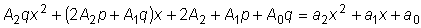 ,
,
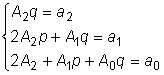 .
.
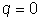 , то частное
решение y* ищем в виде
, то частное
решение y* ищем в виде
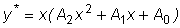 , когда один из корней
характеристического уравнения равен нулю, и в виде
, когда один из корней
характеристического уравнения равен нулю, и в виде 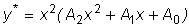 ,
, 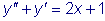 .
.
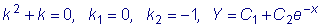 .
. 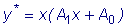 .
. 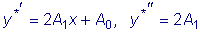 .
. 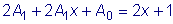 .
. 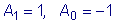 .
Значит, частное решение будет
.
Значит, частное решение будет 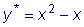 ,
, 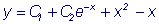 .
.
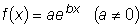 .
.
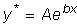 ,
, 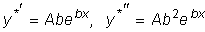 .
. 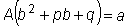 .
. 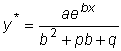 .
.
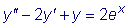 .
.
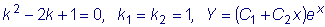 .
. 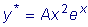 .
.
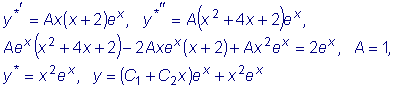 .
.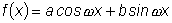 . (a и
b не нули одновременно).
. (a и
b не нули одновременно).
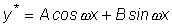 ,
, 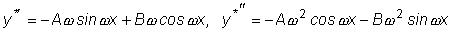 .
.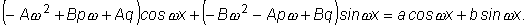 .
. 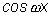 и
и
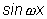 в левой и правой частях
этого равенства должны быть соответственно равны друг другу.
Поэтому
в левой и правой частях
этого равенства должны быть соответственно равны друг другу.
Поэтому 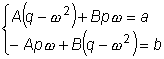 .
.
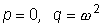
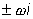 - корни характеристического
уравнения).
- корни характеристического
уравнения).
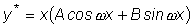 .
. 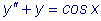 .
.
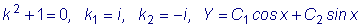 .
.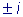 - корни
характеристического уравнения, то частное решение данного уравнения ищем
в виде
- корни
характеристического уравнения, то частное решение данного уравнения ищем
в виде 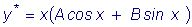 .
. 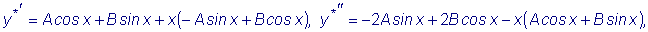
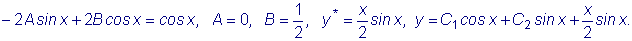 .
.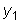 является решением уравнения
является решением уравнения
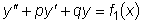 , а
, а
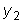 решением уравнения
решением уравнения
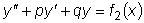 , то
, то
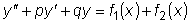 .
. 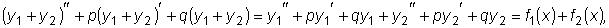 ,
,
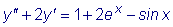 .
. 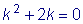
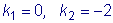 . Следовательно,
. Следовательно, 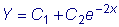 .
.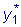 уравнения
уравнения
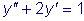 в виде
в виде 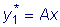 ,
, 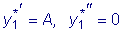 .
. 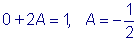 .
. 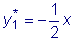 .
.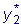 уравнения
уравнения
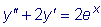 ищем в форме
ищем в форме 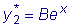 .
. 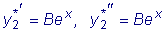 .
. 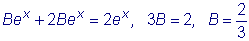 .
. 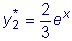 .
.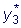 уравнения
уравнения
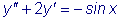 в форме
в форме 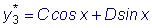 ,
, 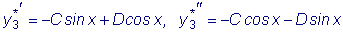 .
. 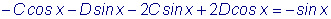 . Отсюда имеем:
. Отсюда имеем: 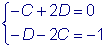 .
. 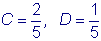 .
. 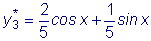 .
. 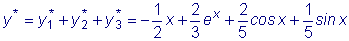 ,
, 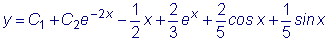 .
.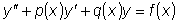 и пусть общим решением соответствующего однородного уравнения
и пусть общим решением соответствующего однородного уравнения
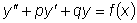 является функция
является функция
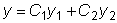 ,
,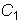 и
и
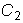 будем считать не произвольными постоянными, а некоторыми, пока
неизвестными функциями от x , т.е. будем считать, что
будем считать не произвольными постоянными, а некоторыми, пока
неизвестными функциями от x , т.е. будем считать, что 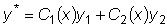 .
.
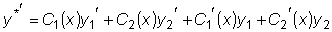 .
.
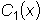 и
и
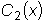 мы будем считать
выбранными так, что
мы будем считать
выбранными так, что 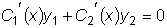 .
. 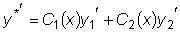
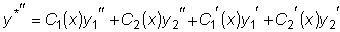 .
. 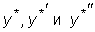
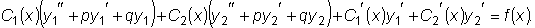 .
. 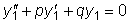 и
и
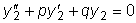 , т.к.
, т.к.
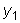 и
и
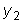 являются решениями однородного уравнения.
являются решениями однородного уравнения.
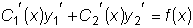 .
. 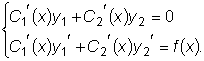 .
. 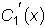 и
и
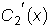 .
. 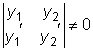 ,
, 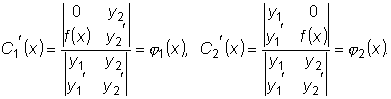 .
. 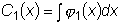 и
и
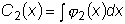 .
. 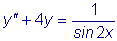 .
.
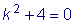
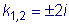 .
.
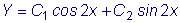 .
.
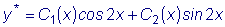 .
.
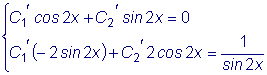
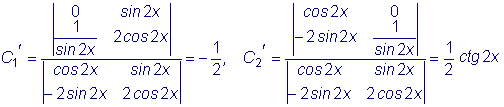 .
.
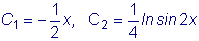 .
.
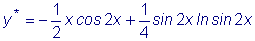 ,
,