Пусть дана однородная система
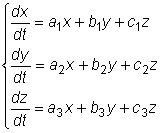 ,
,
где 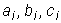 - постоянные.
- постоянные.
Будем искать частные решения системы в виде
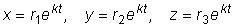 ,
,
где 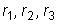 и
k - неопределенные коэффициенты, которые следует найти.
и
k - неопределенные коэффициенты, которые следует найти.
Подставляя эти функции в систему, получим
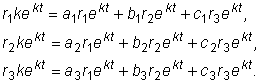
Сокращая на ekt придем к системе линейных
однородных алгебраических уравнений относительно
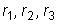 :
:
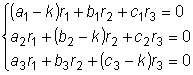 .
.
Чтобы эта система однородных уравнений имела ненулевые решения (только
такие нас и интересуют), необходимо и достаточно, чтобы ее
определитель был равен нулю:
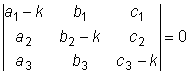 .
.
Раскрывая этот определитель, получим уравнение третьей степени
относительно k . Это уравнение называется характеристическим
уравнением системы дифференциальных уравнений. Отыскав корни этого уравнения и поочередно
подставляя их в исходную систему, определим коэффициенты
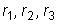 . При этом одно из чисел
. При этом одно из чисел
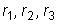 может быть выбрано произвольно, т.к. одно из уравнений исходной системы
дифференциальных уравнений является следствием двух остальных (в силу равенства нулю определителя
этой системы) и система сводится к двум уравнениям с тремя
неизвестными.
может быть выбрано произвольно, т.к. одно из уравнений исходной системы
дифференциальных уравнений является следствием двух остальных (в силу равенства нулю определителя
этой системы) и система сводится к двум уравнениям с тремя
неизвестными.
Таким образом, мы найдем три системы функций, каждая из
которых является решением системы дифференциальных уравнений:
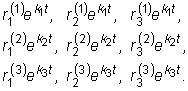
Указанные решения образуют фундаментальную систему и общее решение
системы исходной системы дифференциальных уравнений запишется в виде:
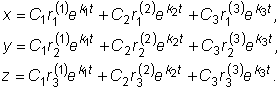
Для получения более общего алгоритма решения однородной системы
дифференциальных уравнений можно воспользоваться её матричным представлением
X' = AX ,
где A - матрица коэффициентов {aij} ,
X = {xj} - вектор неизвестных функций,
X' = {x'j} - вектор производных
неизвестных функций.
Решение системы будет искаться в виде вектора с компонентами - неизвестными
показательными функциями с постоянной k
и неопределенными коэффициентами
X = {rj ekt} = {rj}ekt.
После дифференцирования X , подстановки
X' = ({rj}ekt)' =
k{rj}ekt в систему уравнений и сокращения на
ekt, исходная система примет вид AR = k R , где
R = {rj} .
В терминах векторной алгебры решение матричного уравнения
AR = k R
или однородной системы уравнений
( {aij} - k eij} ) rij = O ,
где
{eij} элементы единичной матрицы E ,
может быть интерпретировано как
нахождение (ненулевого) вектора R = {rj} , такого,
чтобы после умножения его на матрицу A он превратился бы в вектор,
коллинеарный вектору R . Числа k , осуществляющие решение
такой задачи, называются собственными значениями матрицы A ,
а векторы R - собственными векторами этой матрицы.
Нетривиальное решение однородной система уравнений
( {aij} - k {eij} ) rij = O
возможно, если определитель матрицы её коэффициентов равен нулю. Этот определитель назывется характеристическим определителем ,
а уравнение
| {aij} - k {eij} | = O
- характеристическим. Каждому из его корней
k = ki (i = 1,2,...,n) , называемых
характеристическими числами, соответствует одно решение системы дифференциальных
уравнений:
X = {rj} ekit.
Линейная комбинация этих линейно независимых решений в случае, когда они все различны,
(фундаментальная система решений) с произвольными коэффициентами
С1, С2, С3, ..., Сn
образует общее решение системы.

Пример 1.
Найти общее решение системы
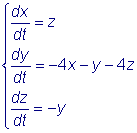 .
.
Система (5) в данном случае имеет вид:
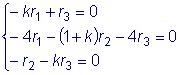 .
.
Характеристическое уравнение
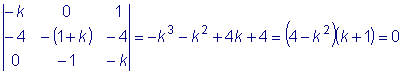
имеет корни
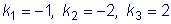 .
.
Для 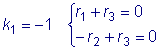 .
.
Решением этой системы будут, например, числа
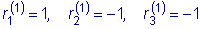 (здесь
(здесь
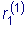 выбрано произвольно).
выбрано произвольно).
Следовательно,
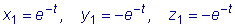 .
.
Для 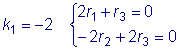 .
.
Решая эту систему, получим
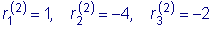 .
.
Тогда
 .
.
Наконец, для 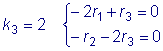 .
.
Здесь можно положить
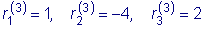
и будем иметь
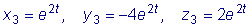 .
.
Общее решение данной системы дифференциальных уравнений таково:
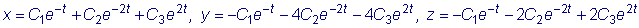 .
.

Вычисление собственных значений
и собственных векторов характеристической матрицы
с использованием системы MathServ

Нахождение корней характеристического уравнения
с использованием системы MathServ

Пример 2.
Решить систему
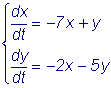 .
.
Чаще системы дифференциальных уравнений записывают в виде:
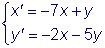 .
.
Составим характеристическое уравнение
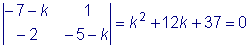
и найдем его корни
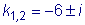 .
Так как эти корни комплексные, система уравнений (5) будет иметь
комплексные коэффициенты и даст комплексные значения для чисел
.
Так как эти корни комплексные, система уравнений (5) будет иметь
комплексные коэффициенты и даст комплексные значения для чисел
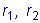 . В этом случае, учитывая
возможность произвольного выбора
. В этом случае, учитывая
возможность произвольного выбора
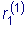 и
и
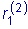 ,
целесообразно сразу положить
,
целесообразно сразу положить
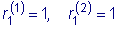 и записав функцию
и записав функцию
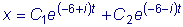
или, что то же самое,
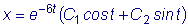 ,
,
найти функцию y , используя первое уравнение системы:
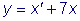 . Для этого найдем
. Для этого найдем

или
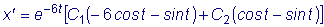 .
.
Подставляя x и
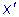 в первое уравнение системы, получим
в первое уравнение системы, получим
 .
.
Общим решением системы будет
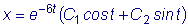
и
 .
.

Вычисление собственных значений
и собственных векторов характеристической матрицы
с использованием системы MathServ

Нахождение корней характеристического уравнения
с использованием системы MathServ
Случай кратных корней характеристического уравнения более сложен, и
здесь рассматриваться не будет.
Подбор частного решения для системы неоднородных дифференциальных
уравнений можно производить, сведя эту систему к одному уравнению
высшего порядка и пользуясь известными приемами.
 Задачи для самостоятельного решения.
Задачи для самостоятельного решения.

