| Темы | Предыдущий пункт | Следующая лекция | Литература | ||
|
|
||

Теория вероятностей |
||
|
13.1.9 Непрерывное вероятностное пространство. Геометрические вероятности Рассмотрим эксперимент с бесконечным числом исходов, которые интерпретируются, как выбор наудачу точки из некоторого множества в n - мерном евклидовом пространстве
Пусть Вероятностью события А назовем число Р(А) определяемое формулой
где в правой части находится n кратный интеграл Римана. Используя свойства интегралов, легко проверяется, что функция Р(А) удовлетворяет аксиомам теории вероятностей. Вместо конечной области G можно рассматривать все n - мерное пространство., а интеграл в этом случае понимать, как несобственный. Функцию Р(А) , определенную на алгебре А, можно продолжить на более широкую систему множеств, содержащую счетные суммы и произведения событий. Построенное вероятностное пространство иногда называют непрерывной вероятностной моделью или непрерывной схемой.
Рассмотрим частный случай общей
непрерывной схемы, положив В этих соотношениях m(G) – мера области G (площадь или объем). При таком выборе функции f(u) формула (1) запишется в следующем виде:
Такое определение вероятности называют геометрическим. Его можно рассматривать, как обобщение классического определения вероятности на случай экспериментов с бесконечным (несчетным) числом исходов.
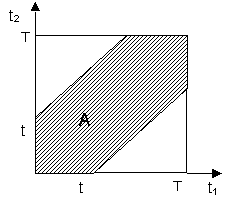
Пример. На обслуживающее устройство в промежуток времени [0, T] должны поступить две заявки. Если разность между моментами поступления заявок меньше t, то вторая заявка теряется. Найти вероятность потери заявки. Решение. Пусть
t1 и t2 –
моменты поступления заявок. Тогда
Для нахождения искомой
вероятности воспользуемся
геометрическим определением. Для чего
вычислим
Замечание. Соответствие выбранной модели случайного явления действительности может быть оценено на основе экспериментов. |
|
|
|
|