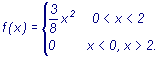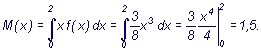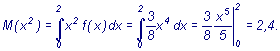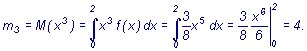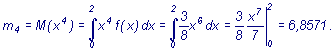| Темы | Предыдущий пункт | Следующая лекция | Литература |
|
|
 Случайные
величины
Случайные
величины
|
|
13.4.4 Числовые характеристики случайных величин Закон распределения полностью характеризует случайную величину с вероятностной точки зрения. Однако во многих задачах оказывается трудно или даже невозможно полностью описать функцию распределения вероятностей. В то же
время для решения многих задач
достаточно знать лишь некоторые
параметры, характеризующие случайную
величину с той или иной точки зрения.
Это напоминает ситуацию, когда взамен
описания мельчайших подробностей
геометрической формы твердого тела
ограничиваются такими его
характеристиками, как длина, ширина,
высота, объем, момент инерции и т. д.
В
теории вероятностей числовыми
характеристиками случайной величины
служат моменты распределения. Они
легко определяются из
экспериментальных данных и позволяют в
общих чертах судить о характере
случайной величины. Для
непрерывных случайных величин моменты
распределения к – ого порядка (к = 1, 2, …)
определяются по формуле
в предположении, что
несобственный интеграл абсолютно
сходится.
Если случайная величина
дискретна и принимает значения при
условии, что ряд в правой части
сходится абсолютно.
Следует
иметь ввиду, что характеризовать
случайную величину при помощи моментов
удается не всегда, так как не для
всякого распределения эти моменты
существуют Математическое ожидание Простейшая числовая
характеристика случайной величины –
момент распределения первого порядка,
определяющая абсциссу центра тяжести
плоской фигуры, ограниченной кривой
распределения и осью абсцисс,
называется математическим ожиданием
или средним значением случайной
величины. В соответствии с общим
определением моментов распределения
математическое ожидание непрерывной
случайной величины Х равно а математическое ожидание
дискретной случайной величины равно Свойства:
Математическое
ожидание суммы двух случайных
величин равно сумме их
математических ожиданий:
Математическое
ожидание произведения двух
независимых случайных величин равно
произведению их математических
ожиданий:
Математическое
ожидание постоянной величины (неслучайной)
равно самой постоянной:
М(с) = с.
Математическое
ожидание отклонения случайной
величины от его математического
ожидания равно 0.
Пример
Найти математическое
ожидание числа бракованных изделий в
выборке из пяти изделий, если случайная
величина Х (число бракованных изделий),
задана рядом распределения
Решение
По
определению Математическое ожидание функции от случайной величины На практике встречаются задачи, в которых случайная величина не выражается числом, а обладает только качественной характеристикой. Например, выпускаемая заводом продукция делится на годную и бракованную. Вынутая наугад из колоды карта характеризуется наименованием и мастью. Принятый радиолокационный сигнал несет информацию о наличии или отсутствии цели и т. п. Однако возможно введение
количественной оценки и для величин
имеющих лишь качественное различие.
Будем рассматривать случайную
величину как результат некоторого
эксперимента. Любой эксперимент
требует определенных затрат и ставится
ради достижения определенной цели.
Исход эксперимента является
желательным или нежелательным в
зависимости от того, насколько
достигается поставленная цель.
Достижение поставленной цели можно
рассматривать как выигрыш или выгоду, а
не достижение – как проигрыш или убыток. И выгоду и
убыток можно выразить числами (например,
суммы денег в рублях).
Таким образом, каждому исходу
эксперимента Это отображение дает
вещественную функцию Для непрерывной
случайной величины
Для
дискретной случайной величины
Пример 2
Вероятность
того, что выпущенный заводом прибор
окажется бракованным, равна р.
Какова средняя прибыль, приходящаяся
на один прибор, если а –
себестоимость, b
– цена продукции. Решение
Прибыль, приходящаяся на один прибор
равна (b
– a),
ей соответствует вероятность того, что
прибор не бракован (1 – р). Обозначая
среднюю прибыль через Q,
находим
Q
= (b – a)(1 – p) – ap = b(1 – p) – a. Если
рассматривать математическое ожидание
как средний выигрыш при большом числе
экспериментов, то считается, что
эксперимент проводить целесообразно,
если
Дисперсия.
Среднеквадратичное отклонение
Разность
между
случайной величиной и ее средним
значением называется отклонением случайной величины. Моменты
распределения вероятностей отклонения
случайной величины называют центральными
и обозначают
В отличие от моментов Для
дискретной случайной величины
центральные моменты распределения
определяются соответствующими
суммами
Если среднее значение
случайной величины равно нулю, то Центральный момент
распределения второго порядка
называется дисперсией случайной
величины Х и определяется формулами:
для
непрерывной случайной величины
для дискретной случайной
величины
Дисперсия
характеризует отклонения отдельных
значений случайной величины от
математического ожидания, то есть
является мерой рассеяния случайной
величины. Чем меньше дисперсия, тем
более тесно концентрируются отдельные
значения случайной величины вблизи
математического ожидания.
Недостатком
дисперсии является то, что она имеет
размерность квадрата случайной
величины. Этого недостатка лишено средне
квадратичное отклонение случайной
величины, которое определяется
формулой Его еще называют
стандартным отклонением. Свойства дисперсии:
Пример 3
Вычислить дисперсию числа
бракованных изделий для распределения
Решение.
В
примере 1
для этого
распределения найдено
М(х) = 1,25, поэтому по определению
дисперсии имеем Асимметрия
и эксцесс
Математическое
ожидание и дисперсия не отражают всех
особенностей кривой распределения.
Одной из таких особенностей является
симметрия или асимметрия кривой
распределения относительно оси,
проходящей через тяжести. В любом
симметричном распределении
центральный момент произвольного
нечетного порядка равен нулю (это
следует из их определения). Поэтому
простейший из нечетных моментов (центральный
момент третьего порядка) может в первом
приближении служить характеристикой
асимметрии распределения. Центральный
момент третьего порядка
может быть выражен через
начальные моменты первых трех порядков
За характеристику
несимметричности распределения (асимметрии
или скошенности) принимают
безразмерную величину – отношение
третьего центрального момента к кубу
среднего квадратического отклонения: которая
называется коэффициентом асимметрии.
Центральный
момент четвертого порядка при данной
дисперсии может служить
характеристикой удельного веса
больших отклонений от математического
ожидания, то есть определять характер
максимума в точке М(х) симметричного
распределения – островершинность или
плосковершинность кривой
распределения. В качестве
характеристики сглаженности кривой
распределения используют безразмерную
величину
называемую
коэффициентом эксцесса.
Центральный
момент четвертого порядка может быть
выражен через начальные моменты
следующим образом
Пример 4
Случайная величина Х задана
плотностью распределения
Найти математическое
ожидание, дисперсию, ассиметрию и
эксцесс
Решение
Находим математическое
ожидание Определим Тогда
дисперсия определяется формулой Вычисляем начальные моменты
первого, второго, третьего и четвертого
порядков
Центральные моменты
третьего и четвертого порядков находим
через начальные моменты
Таким образом, коэффициент
асимметрии будет равен
|
|
|
|
|