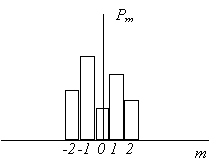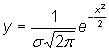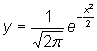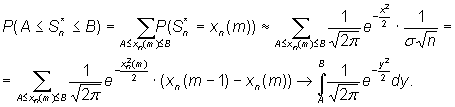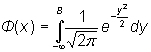Рассматривая единичное случайное событие А, имеющее вероятность Р(А) нельзя высказывать никаких суждений относительно того, наступит или нет это событие в данном эксперименте. Исключение составляют случаи, когда вероятность события А близка к единице или к нулю. Если вероятность Р(А) события А мала (или близка к единице), можно утверждать, что в данном единичном эксперименте событие А не произойдет (или произойдет). То есть в практической деятельности можно руководствоваться следующим принципом: если вероятность Р(А) события А мала (или близка к единице), то практически можно поступать так, как если бы событие А было невозможным (или достоверным), то есть считать событие А практически невозможным (или практически достоверным).

Ответ на вопрос – насколько малой должна быть вероятность Р(А), чтобы событие А можно было считать практически невозможным – может дать только практика. Например, если условия эксплуатации прибора допускают в случае его поломки замену другим, и вероятность Р(А) = 0,01 (событие А означает выход прибора из строя), то возможностью выхода его из строя можно пренебречь и считать событие А практически невозможным.

Когда условия эксплуатации не допускают замену прибора, а выход его из строя влечет за собой серьезные последствия, то вероятностью 0,01 пренебречь нельзя и нельзя считать практически невозможным событием выход прибора из строя.

Таким образом, в практических применениях теории вероятностей особо важную роль играют события с вероятностями, близкими к нулю или к единице. Достаточно малую вероятность, при которой событие можно считать практически невозможным, называют уровнем значимости. На практике, обычно, принимают уровни значимости заключенные между 0,01 и 0,05. Следует иметь в виду, что принцип практической достоверности применим только к массовым явлениям, а не к одному единственному.

Центральная предельная теорема 

Рассмотрим сумму независимых случайных величин , имеющих один и тот же закон распределения и принимающих целочисленные значения

Распределение  p_m = P(x_k = m) каждой из величин можно изобразить системой прямоугольников, середина основания которых есть точка m, длина основания равна 1, а площадь есть p_m . Получится совершенно произвольная система прямоугольников, подчиненная лишь условию – сумма всех площадей равна единице.

Попытаемся изобразить таким же образом вероятности значений суммы при довольно большом n. Нам это не удастся, так как даже если случайные величины принимали всего два значения 0 и 1, то значениями суммы S_n могут быть числа от 0 до n, которые при большом n просто не поместятся на рисунке. Возникает необходимость сделать линейное преобразование оси абсцисс и вместо значений случайной величины откладывать значения величины

где a_n и b_n - некоторые числа, зависящие от n.

Лаплас обнаружил, что получится удивительное, если положить

Случайная величина

является нормированной суммой с

Значениями величины будут числа

причем для любого целого m 

.

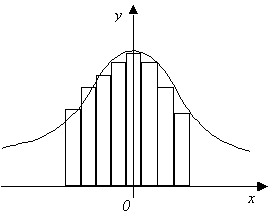
Отложим по оси абсцисс значения и изобразим вероятности этих значений прямоугольниками, середины оснований которых лежат в точках , длины оснований равны расстоянию между соседними точками, а площади равны

Высоты этих прямоугольников равны

При этом произойдет удивительное. Верхние основания этих прямоугольников почти точно лягут на кривую, задаваемую уравнением 

Иначе говоря, при имеем

.

При этом очевидно

Вводя функцию

называемую функцией Лапласа, получим

Таким образом, мы получили, что для широкого класса независимых случайных величин предельный закон распределения их нормированной суммы вне зависимости от типа распределения слагаемых стремится к нормальному закону распределения. В этом и заключается смысл центральной предельной теоремы. Она может быть строго доказана.

Центральная предельная теорема дает математически строгое описание условий, порождающих механизм нормального закона распределения – значение исследуемой непрерывной случайной величины формируется под воздействием большого числа независимых случайных факторов, сила воздействия каждого из которых не может преобладать среди остальных, а характер воздействия – аддитивный.