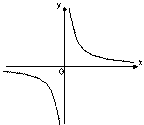| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|
Лекция 3.1. 
Предел. Непрерывность функции. |
|
|
|
|
|
3.1.11. Точки разрыва функции и их классификация
|
|
Если рассмотреть график функции
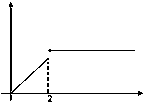
то ясно видно, что он как бы “разрывается” на отдельные кривые. Аналогично можно рассмотреть функцию, изображенную на рисунке в окрестности точки 2.
Говорят, что во всех указанных точках соответствующие функции становятся разрывными.
Точка x 0 называется точкой разрыва функции y = f(x), если она принадлежит области определения функции или её границе и не является точкой непрерывности.В этом случае говорят, что при x= x0 функция
разрывная. Это может произойти, если в точке x0 функция
не определена или не существует предел
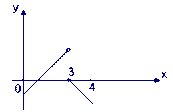
Примеры. 1. Рассмотрим функцию: 
Эта функция определена во всех точках отрезка [0, 4] и её значение при x = 3 равно 0. Однако, в точке x = 3 функция имеет разрыв, т.к. она не имеет предела при x = 3:
Следует отметить, что f(x) непрерывна во всех остальных точках отрезка [0, 4]. При этом в точке x = 0 она непрерывна справа, а в точке x = 4 – слева, т.к.
2. Функция
Точки разрыва функции можно разбить на два типа. Точка разрыва x0 функции f(x) называется
точкой разрыва первого рода, если существуют оба односторонних
конечных предела В первом примере точка х=3 является точкой разрыва первого рода. В примере 2 все точка разрыва x = 0 являются точкой разрыва второго рода. |
в окрестности точки x = 0 
, или если предел существует, но
.
разрывна при x
= 0. Действительно:
, но они не равны между собой или не равны значению функции в
точке x0, т.е. f(x0). Точка разрыва,
не являющаяся точкой разрыва первого рода, называется точкой разрыва
второго рода.
|
|