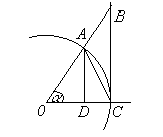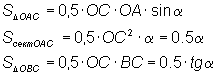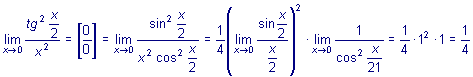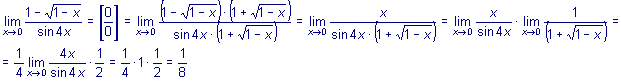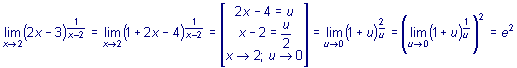| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Предел. Непрерывность функции. |
|
|
|
|
|
3.1.8. Замечательные пределы
|
|
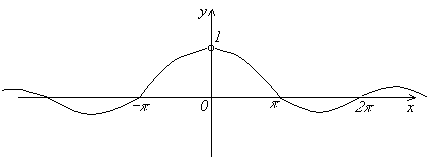
Первый замечательный предел Функция
Однако, можно найти предел этой функции при
Приведем доказательство записанной формулы.
Рассмотрим
окружность радиуса 1 и предположим, что угол
Так как указанные площади соответственно равны
Следовательно, Разделим все члены неравенства на
sin
Но Выведенная формула и называется первым замечательным пределом. Таким образом, первый замечательный предел служит для раскрытия
неопределенности
Примеры 1.
2.
3.
Второй замечательный предел Второй замечательный предел служит для раскрытия неопределенности
Обратим внимание на то, что в формуле для второго замечательного предела в показателе степени должно стоять выражение, обратное тому, которое прибавляется к единице в основании (так как в этом случае можно ввести замену переменных и свести искомый предел ко второму замечательному пределу).
Примеры
1.
2.
3.
|
|
|