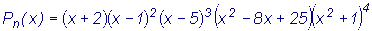Вспомним некоторые свойства многочленов с действительными коэффициентами.
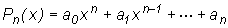 - многочлен n-ой степени.
Степенью многочлена называют максимальную степень при x.
Корнем
многочлена называют такое число, подстановка которого обращает многочлен
в 0.
- многочлен n-ой степени.
Степенью многочлена называют максимальную степень при x.
Корнем
многочлена называют такое число, подстановка которого обращает многочлен
в 0.
Рассмотрим виды простейших многочленов:
I. Линейный: x-a . Корень многочлена a, его нельзя
разложить на множители.
II. Квадратный трехчлен: x2 + px + q. При наличии
действительных корней x1 и x2
можно разложить на множители.  .
.
III. Многочлены степени 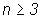 .
.
 Теорема
Теорема
Всякий многочлен с действительными коэффициентами степени выше
второй может быть представлен в виде произведения линейных и квадратных
сомножителей в виде Pn(x)=(x-a)k1(x-b)k2
...(x2 + p1x + q1)t1(x2 + p2x + q2)t2...
где a, b - корни многочлена кратностей соответственно k1 и
k2. (Если k1=1, то a - простой корень, при k1>1 - a - кратный корень). У квадратных трехчленов действительных корней нет.

Пример

 .
.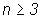 .
.