| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Дифференциальные уравнения высших порядков |
|
|
|
|
6.2.4. Линейные однородные уравнения второго порядка |
|
Рассмотрим линейное однородное уравнение второго порядка, т.е.
уравнение
Свойство 1 Свойство 2 Две функции
Примеры
1. Функции y1 = e x и
y2 = e - x
линейно независимы при всех значениях x , т.к.
Теорема 1.
Если функции
Доказательство.
Если
Замечание.
Теорема 2.
Если определитель Вронского, составленный для решений
Доказательство.
Пусть определитель Вронского обращается в ноль в точке
Следствия.
1. Если определитель Вронского, фигурирующий в теоремах, равен нулю при
каком-нибудь значении x=
2. Если решения
3. Если определитель Вронского отличен от нуля хотя бы в одной точке,
то решения
Теорема 3.
Если
Доказательство.
Как известно, функция
Примеры
Пример 1.
Общим решением уравнения
Следовательно, функции sinx и cosx линейно независимы.
В этом можно убедиться, рассмотрев отношение этих функций:
Пример 2.
Решение
y = C1 e x + C2 e - x
уравнения
Пример 3.
Уравнение
Замечание
Мы установили, что общее решение линейного однородного уравнения
второго порядка можно получить зная два каких-либо линейно независимых
частных решения этого уравнения. Однако, не существует общих методов
для нахождения таких частных решений в конечном виде для уравнений с
переменными коэффициентами. Для уравнений с постоянными
коэффициентами такой метод существует и будет рассмотрен нами позднее.
|
|
|
|
|
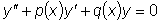 и установим некоторые
свойства его решений.
и установим некоторые
свойства его решений. 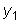 является решением
линейного однородного уравнения,
то C
является решением
линейного однородного уравнения,
то C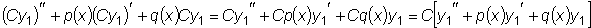 ,
, 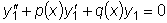 , т.к.
, т.к.
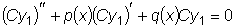
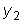 являются решениями рассматриваемого уравнения, тогда
являются решениями рассматриваемого уравнения, тогда 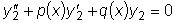 .
. 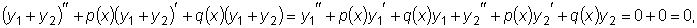 , т.е.
, т.е.
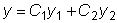 , зависящее от двух
произвольных постоянных, т.е. от такого количества постоянных, какое
должно содержать общее решение уравнение второго порядка. Но будет ли
это решение общим, т.е. можно ли путем выбора произвольных постоянных
, зависящее от двух
произвольных постоянных, т.е. от такого количества постоянных, какое
должно содержать общее решение уравнение второго порядка. Но будет ли
это решение общим, т.е. можно ли путем выбора произвольных постоянных
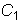 и
и
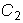 удовлетворить произвольно
заданным начальным условиям?
удовлетворить произвольно
заданным начальным условиям? 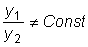 .
. 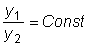 на всем интервале.
на всем интервале.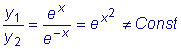 .
. 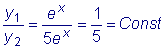 .
. 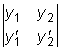 ,
называемый определителем Вронского данных функций,
тождественно равен нулю на этом интервале.
,
называемый определителем Вронского данных функций,
тождественно равен нулю на этом интервале.
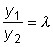 ,
, 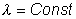 , то
, то
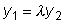 и
и
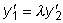 .
. 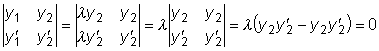 .
. 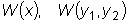 .
. 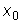 , т.е.
, т.е.
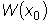 =0,
=0,
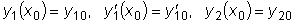 и
и
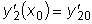 .
. 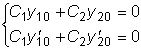
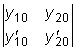 совпадает со значением
определителя Вронского при
совпадает со значением
определителя Вронского при
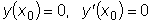 , т.к.
, т.к.
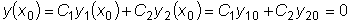 и
и
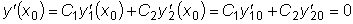 .
.
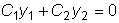 . Откуда следует, что
. Откуда следует, что 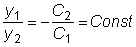 ,
,
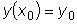 и
и
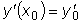 ,
, 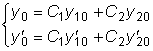 .
. 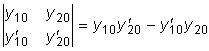
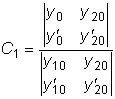 ;
;
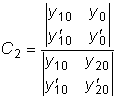 .
. 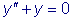 является решение
является решение
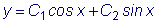 .
.
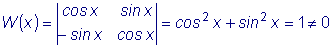 .
.
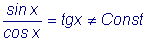 .
.
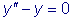 является общим, т.к.
является общим, т.к.
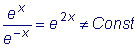 .
.
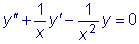 ,
, 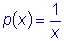 и
и
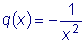
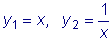
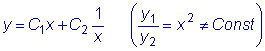 .
.