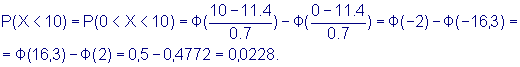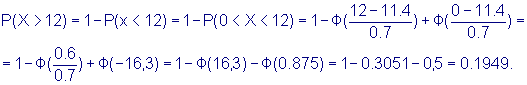| Темы | Предыдущий пункт | Следующий пункт | Литература | |||||||
|
|
|||||||
 Распределение
случайных величин
Распределение
случайных величин
|
|||||||
|
13.5.4 Нормальное распределение Это распределение занимает центральное место в теории и практике верятностоно - -статистических исследований. Механизм формирования нормально распределенных случайных величин заключается в следующем. Значение исследуемой непрерывной случайной величины формируется под воздействием большого числа независимых случайных факторов, причем сила воздействия каждого отдельного фактора мала и не может превалировать в среде остальных, а характер воздействия - аддитивный. Главной особенностью нормального закона распределения является то, что он является предельным законом, к которому приближаются другие законы распределения. Важность нормального закона распределения определяется рядом причин: 1. Такое распределение служит хорошей математической моделью для ряда наблюдаемых случайных явлений и этот факт можно строго доказать для многих ситуаций. 2. Нормальное распределение принадлежит к числу немногих, позволяющих описывать ситуации с произвольным числом случайных величин. 3. Любые линейные комбинации нормальных случайных величин, также являются нормальными. Для большинства других случайных величин это утверждение не справедливо. 4. Нормальный (гауссовский) случайный процесс может быть полностью описан (в статистическом смысле) при помощи только первого и второго моментов. Для других процессов это утверждение не верно. 5. Исчерпывающий статистический анализ в ходе системного анализа как для линейных, так и для нелинейных преобразований случайных прочесов часто удается выполнить, только если эти процессы нормальные (гауссовские). Функция плотности нормального закона распределения имеет вид.
Функция распределения
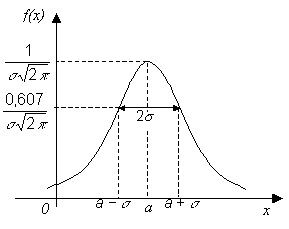
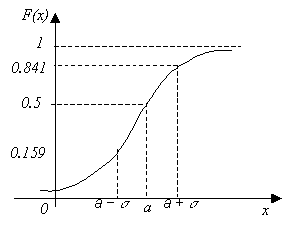
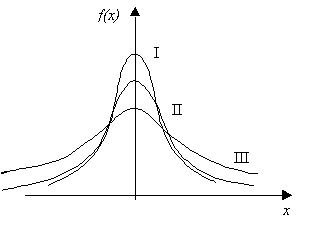
Графики плотности и функции
распределения вероятностей
нормального закона приведены на
рисунках 1 и 2. График плотности
нормального распределения называют
нормальной кривой. Она представляет
собой колоколообразную фигуру,
симметричную относительно прямой х = а
и асимптотически приближающуюся к оси
абсцисс при Найдем математическое ожидание и дисперсию случайной величины, подчиняющейся нормальному закону.
Так как Итак, имеем М(х) = а.
Таким образом имеем
Свойства нормального распределения. Свойство 1. Функция плотности
нормального распределения в точке х = а
имеет максимум, равный Свойство 2. График функции плотности f(x) симметричен относительно прямой, проходящей через точку а: х = а. Из этого свойства следует равенство для нормально распределенной случайной величины моды, медианы и математического ожидания. Свойство 3. Кривая распределения
имеет две точки перегиба с
координатами При изменении параметра а форма
нормальной кривой не изменяется,
график кривой сдвигается влево или
вправо. При изменении же параметра
Функция плотности распределения с
параметрами а = 0, Вероятность попадания в заданный интервал. По определению имеем
где Окончательно получим:
Если промежуток Итак
В частности при
Пример 1 Найти вероятность того, что емкость
конденсатора будет находиться в
пределах Решение.
Пример 2 Размер детали задан полем допуска 10 - 12 мм. Оказалось, что средний размер деталей равен 11,4 мм, а среднее квадратичное отклонение 0,7 мм. Считая, что размер детали подчиняется нормальному закону, определить вероятность появления брака по заниженному и по завышенному размеру. Решение По условию задачи
имеем М(х) = а = 11,4;
Аналогично находим
Как уже отмечалось выше, нормальный
закон распределения широко
используется в экономике, технике,
медицине, биологии и. т. д. Однако кроме
этого нормальное распределение имеет
большое теоретическое значение: с его
помощью выведен целый ряд других
важных распределений, построены
различные статистические критерии и.т.п.
(
|
|
|
|
|
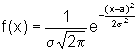 .
.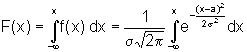 .
.
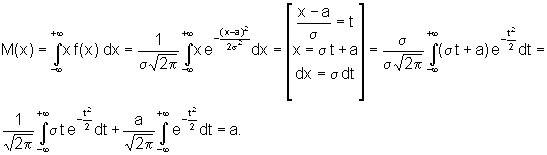 .
.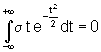 (под
знаком интеграла с симметричными
пределами стоит нечетная функция),
(под
знаком интеграла с симметричными
пределами стоит нечетная функция), 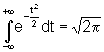 .
. 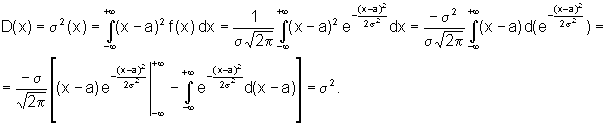 Первое
слагаемое
Первое
слагаемое 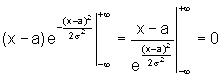 ,
так как экспонента растет быстрее, чем (х
- а) при
,
так как экспонента растет быстрее, чем (х
- а) при 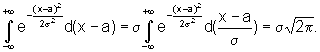
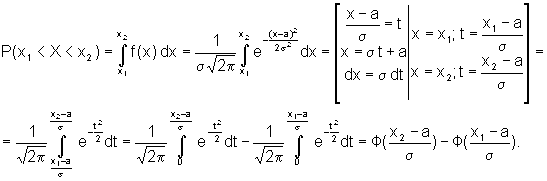
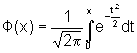 -
функция Лапласа, ее значения
табулированы. Функция Лапласа нечетная
функция, то есть Ф(-х) = Ф(х).
-
функция Лапласа, ее значения
табулированы. Функция Лапласа нечетная
функция, то есть Ф(-х) = Ф(х).