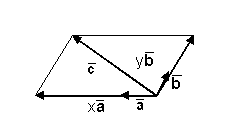| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Векторная алгебра |
|
|
1.2.4. Векторный базис на плоскости и в пространстве, координаты вектора.
Определение 1.
Линейной комбинацией векторов
Определение 2. Заданные векторы называются линейно зависимыми, если какой-либо из этих
векторов является линейной комбинацией остальных; в противном случае эти
векторы называются линейно независимымыми (между собой). Если вектор
представлен в виде линейной комбинации некоторых векторов, то говорят,
что он разложен по этим векторам. Так, например, если вектор
Рис. 2.12. Необходимым и
достаточным условием линейной зависимости двух Поэтому на плоскости можно указать два линейно независимых вектора, но всякие три вектора уже линейно зависимы. Определение 3.
Совокупность двух линейно независимых векторов
Определение 4.
Базис ( В ортонормированном
базисе на плоскости единичные векторы обозначаются через
Подобным образом в
пространстве можно указать уже три линейно независимых вектора ( любая
тройка некомпланарных векторов)
Числа x, y, z называются
координатами вектора
Любые четыре вектора
в трехмерном пространстве линейно зависимы. При сложении двух векторов
|
|
|
|
|