| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Элементы линейной алгебры |
|
|
1.1.3 Определители. Определители используются не только в теории линейных алгебраических уравнений. Они широко применяются в других разделах высшей математики, в теоретической механике, физике и самых разнообразных приложениях математических методов для сокращения записей и удобства вычислений. Рассмотрим, прежде всего, определители 2-го порядка. Определитель 2-го
порядка Правило вычисления определителей 2-го порядка легко запомнить с помощью следующей схемы: из произведения элементов главной диагонали вычитается произведение элементов побочной диагонали.
Пример 1. Вычислить
определитель
Решение:
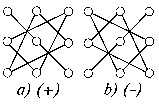
Определитель 3-го порядка есть число, записанное в виде: Один из способов вычисления определителя - по правилу "треугольников" легко понять и запомнить с помощью схем а) и b) рис. 1.1.
При вычислении с плюсом берутся произведения чисел на главной диагонали и в вершинах двух треугольников с основаниями, параллельными этой диагонали. С минусом берутся произведения чисел на побочной диагонали и в вершинах двух треугольников с основаниями, параллельными этой диагонали. Определитель 3 - го порядка можно вычислять также по правилу Саррюса, приписывая к определителю два первых столбца и умножая элементы на диагоналях, параллельных главной со знаком плюс, а на параллельных побочной со знаком минус и складывая их после этого:
Пример 2. Вычислить
определитель Решение: Рассмотрим еще один способ вычисления определителя 3 - го порядка. Он является универсальным, т.к. может быть применен для вычисления определителя любого порядка:
Данная формула
сводит задачу вычисления определителя третьего порядка к вычислению трех
определителей второго порядка. Она называется "формулой разложения
определителя по элементам первой строки". Легко видеть, что такое же
разложение можно сделать по элементам любой другой строки или столбца (проверьте
это). Определитель второго порядка, стоящий у элемента
Выражение
Как уже говорилось, данное правило вычисления определителя справедливо для определителя любого порядка, например, разложение определителя по элементам i строки записывается так:
Пример 3.
Из приведенного примера видно, что вычисление определителей является весьма трудоемким делом. Рассмотрим свойства определителей, позволяющие упростить процедуру их вычисления. Для упрощения записей будем доказывать их для определителей второго порядка. В общем случае они доказываются методом индукции, начиная с n = 2. Свойства определителей: Величина определителя: 1) равна нулю, если элементы какого - либо столбца или строки равны
нулю
2) равна нулю, если соответствующие элементы двух строк (столбцов)
равны 3) меняет знак, если поменять местами строки (столбцы)
4) увеличивается в k раз, если элементы какого - либо столбца (строки) увеличить в k раз;
5) не меняется при замене строк соответствующими столбцами:
6) не меняется, если элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель
7) линейное свойство определителя (обобщающее) - если в определителе какая-либо строка (столбец) является линейной комбинацией двух строк (столбцов), то определитель равен линейной комбинации определителей с теми же коэффициентами. Данное свойство легче написать формулой, чем пояснить словами
Все первые шесть свойств являются следствиями данного линейного свойства определителя. Используя эти свойства, можно значительно упростить процедуру вычисления определителя. Прямое вычисление определителя, использующее его явное выражение через его элементы, редко применяется на практике из-за его трудоемкости. Если определитель имеет так называемый треугольный вид, то он вычисляется как произведение чисел, стоящих на главной диагонали:
Из свойств 2, 6 определителя следует, что его можно приводить к треугольному виду и вычислять тем же методом исключения Гаусса, которым мы решали систему. |
|
|
|
|
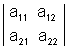 - это число, записанное в виде
- это число, записанное в виде
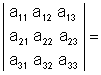
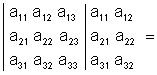
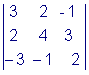
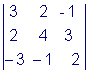 =
= 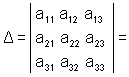
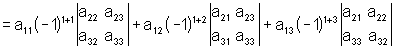
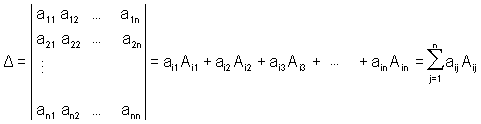 .
.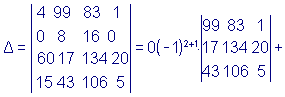
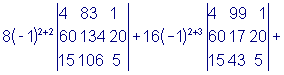
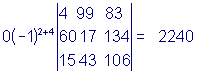
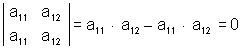 ;
;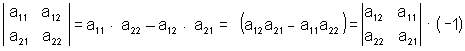 ;
;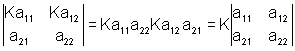
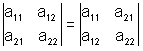 ;
;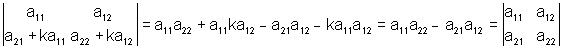
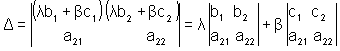 .
.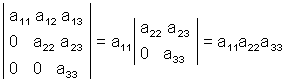 .
.