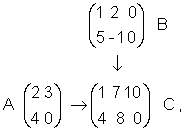| Темы | Предыдущий пункт | Следующий пункт | Литература | |||||
|
|
|||||

Элементы линейной алгебры |
|||||
|
1.1.4 Система из m уравнений с n неизвестными. Системы линейных алгебраических уравнений, в которых число уравнений не совпадает с числом неизвестных, называются прямоугольными
Прежде чем решать и исследовать системы, займемся введением более удобных, кратких форм записи. В математике таблица, составленная из каких-либо элементов, называется матрицей. Если элементы матрицы - числа, то матрица называется числовой. Число строк m и число столбцов n определяют размеры матрицы A и называются ее размерностью. Записывается
Например,
матрица - строка
Для того, чтобы матрицы использовать при записи исходной системы уравнений, нужно определить операции сложения матриц и умножения матрицы на число. Суммой двух матриц A и B одинакового размера называется матрица C (записывается A + B = C) того же размера, элементы которой равны сумме соответствующих элементов матриц A и B. Матрицы A и B называются равными (записывается A = B), если эти матрицы имеют одинаковую размерность и их соответствующие элементы равны. Произведением
матрицы A на число
Из определения операций сложения матриц одинакового размера и умножения матрицы на число вытекают следующие очевидные свойства данных операций, которые понадобятся нам в дальнейшем. Свойства операции сложения матриц 1.Коммутативность. 2.Ассоциативность. 3.Существование нуля: существует такая матрица (обозначим ее O, что A + O = A. 4.Существование противоположного элемента: для любой матрицы A существует матрица , обозначаемая - A, что A + (- A ) = O. Свойства умножения матрицы на число 1.Ассоциативность:
2.Дистрибутивность по отношению к сумме чисел
3.Дистрибутивность по отношению к сумме матриц
Если множество каких-либо математических объектов с определенными на нем операциями сложения объектов и умножения объекта на число, удовлетворяют перечисленным свойствам, то говорят, что данные объекты образуют линейное пространство. Поэтому можем сказать, что множество матриц одинакового размера образует линейное пространство. Таблицу из коэффициентов при неизвестных в уравнении (1.6) обозначим матрицей
Неизвестные поместим
в матрицу-столбец
Систему линейных алгебраических уравнений тогда можно записать в виде:
Тот факт, что это запись нашей системы, подсказывает нам, как будет далее определено произведение двух матриц. Произведением
матрицы A размера
Обратите внимание на то, что умножать можно не любые матрицы, а только те, у которых число столбцов первого сомножителя совпадает с числом строк второго сомножителя.
Примеры. 1.
2. 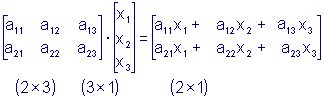 . .
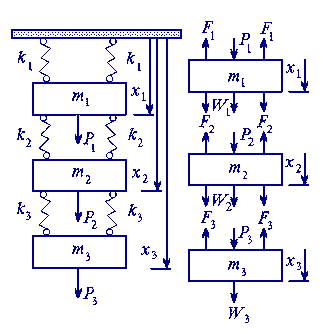
4. Механическая система включаeт в себя массы и пружины и соединена как показано на рис. 1.2. . Составить систему уравнений в матричной форме, описывающую состояние системы грузов.
Решение На элементы системы, характеризуемые положением
действуют граничные
силы силы натяжения
пружин где Математическая модель определяется на основе второго закона Ньютона: тело находится в равновесии, если сумма действующих на него сил равна нулю (рис. 1.2. справа). После суммирования всех сил, действующих на каждое из трех тел, получим:
где
После подстановки этих величин получим линейную систему уравнений:
В матричной форме она принимает вид: 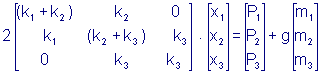 . .
Продемонстрируем один из приемов запоминания правила умножения матриц. Он основан на удобном расположении перемножаемых матриц на бумаге. Если нам нужно найти
C=AB,
тогда при умножении вы уменьшите вероятность появления случайных арифметических ошибок. Можно показать, что умножение матриц обладает свойствами: 1.Ассоциативность: (AB)C=A(BC). 2.Дистрибутивность: A(B+C)=AB+AC;(B+C)A=BA+CA. Из приведенных
примеров видно: умножение матриц не коммутативно, т.е. в общем случае
|
|
|
|
|
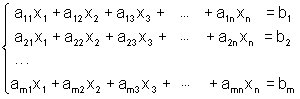
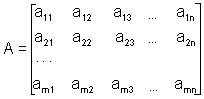 .
.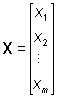 , свободные члены в
, свободные члены в
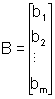 .
.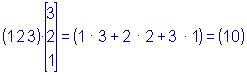 ;
; 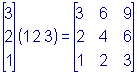 .
.
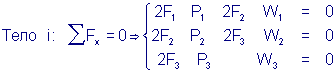 ,
,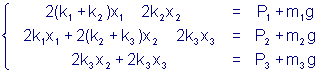 .
.