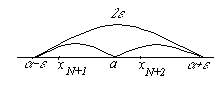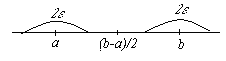ODE Lecture 6.1.

Темы \| Предыдущий пункт \| Следующий пункт \| Литература

Лекция 3.1. Предел. Непрерывность функции.

3.1.2. Предел числовой последовательности

В дальнейшем курсе математики понятие предела будет играть фундаментальную роль, так как с ним непосредственно связаны основные понятия математического анализа – производная, интеграл и др.

Начнем с понятия предела числовой последовательности.

Число a называется пределом последовательности x = {x_n}, если для произвольного заранее заданного сколь угодно малого положительного числа ε найдется такое натуральное число N, что при всех n > N выполняется неравенство |x_n - a| < ε.

Если число a есть предел последовательности x = {x_n}, то говорят, что x_n стремится к a, и пишут

Чтобы сформулировать это определение в геометрических терминах введем следующее понятие.

Окрестностью точки x₀ называется произвольный интервал (a, b), содержащий эту точку внутри себя. Часто рассматривается окрестность точки x₀, для которой x₀ является серединой, тогда x₀ называется центром окрестности, а величина (b–a)/2 – радиусом окрестности.

Итак, выясним, что же означает геометрически понятие предела числовой последовательности. Для этого запишем последнее неравенство из определения в виде

Это неравенство означает, что все элементы последовательности с номерами n>N должны лежать в интервале (a – ; a + ).

Следовательно, постоянное число a есть предел числовой последовательности {x_n}, если для любой малой окрестности с центром в точке a радиуса ( – окрестности точки a) найдется такой элемент последовательности с номером N, что все последующие элементы с номерами n > N будут находиться внутри этой окрестности.

Пример

Пусть переменная величина x последовательно принимает значения

Докажем, что предел этой числовой последовательности равен 1. Возьмем произвольное положительное число Нам нужно найти такое натуральное число N, что при всех n > N выполняется неравенство |x_n - 1| < . Действительно, т.к.

то для выполнения соотношения |x_n - a| < достаточно, чтобы или . Поэтому, взяв в качестве N любое натуральное число, удовлетворяющее неравенству , получим что нужно. Так если взять, например, , то, положив N = 6, для всех n > 6 будем иметь .

Сделаем несколько замечаний.

Замечание 1. Очевидно, что если все элементы числовой последовательности принимают одно и то же постоянное значение x_n = c, то предел этой последовательности будет равен самой постоянной. Действительно, при любом всегда выполняется неравенство |x_n - c| = |c - c| = 0 < .

Замечание 2. Из определения предела следует, что последовательность не может иметь двух пределов. Действительно, предположим, что и одновременно . Возьмем любое и отметим окрестности точек a и b радиуса (см. рис.). Тогда по определению предела, все элементы последовательности, начиная с некоторого, должны находиться как в окрестности точки а, так и в окрестности точки b, что невозможно.

Замечание 3. Не следует думать, что каждая числовая последовательность имеет предел. Пусть, например, переменная величина принимает значения . Несложно заметить, что эта последовательность не стремится ни к какому пределу.