| Темы | Предыдущий пункт | Литература |
|
|

Векторная алгебра |
|
1.2.11 Линейное пространство. В современной математике пространство определяется как множество однородных объектов (предметов, явлений, состояний и т.п.), для которых определены некоторые операции, подчиняющиеся определенным ограничениям. Например, трехмерное цветовое пространство, векторы которого соответствуют цветовым ощущениям и определяются тремя компонентами (базис пространства) - интенсивностями красного, зеленого и синего цветов. Состояние физической системы, описываемое некоторой совокупностью переменных (токи и напряжения электрической цепи, температуры и концентрации веществ в химическом реакторе и т.п.), можно представить вектором n-мерного пространства и называется пространством переменных состояний. Элементами абстрактных пространств могут быть функции, матрицы, некоторые системы чисел и т.д., а , в частности, и обычные векторы. Пусть задано
некоторое множество R, элементами которого являются объекты
Пусть задана вторая
операция, которая каждому элементу
Множество R назовем линейным пространством, если для его элементов введены две операции ”сложение” и “умножение на число”, удовлетворяющие следующим условиям: 1)
2)
3) для любого элемента
4) для каждого
5) 6) 7) 8) Примеры линейных пространств 1) Множество всех вещественных чисел с обычными операциями сложения и умножения. 2) Арифметическое n-мерное векторное пространство. 3) Множество прямоугольных матриц размера
4) Множество всех вещественных непрерывных на отрезке
Пример 1. Показать, что множество функций вида
Решение: Сумма двух функций
есть функция того же множества. Действительно, где
Аналогично,
где Выполнимость
условий, характеризующих линейное пространство, очевидна; следовательно,
данное множество функций образует линейное пространство. Система
векторов
Так как любая
функция f данного
множества линейно выражается через
Пример 2. Найти размерность
линейного пространства, порожденного векторами
Решение: Найдем максимальное число линейно независимых векторов; для чего составляем матрицу, строками которой являются векторы
Ранг этой
матрицы, как нетрудно подсчитать, равен двум, причем отличным от нуля
минором второго порядка будет минор
Интересный пример
линейных пространств дает органическая химия. Совокупность веществ можно
рассматривать как множество, элементами которых являются атомы, молекулы
или другие образования. Отображение этих множеств на множество чисел
осуществим следующим образом. Допустим у нас имеются соединения из
атомов углерода
C и водорода H. Каждому соединению
Все соединения
В общем случае
задана конечная совокупность n атомов,
из которых построены молекулы
рассматриваемого множества. Обозначим
Введем правила сложения и умножения на число, которые вытекают из закона сохранения вещества
Совокупность молекул
Если представить
совокупности атомов
то предыдущие равенства можно записать в следующем виде
или в виде
Например,
совокупность трех молекул
Подобным образом большой класс органических соединений - углеводороды - можно рассматривать состоящим из атомов всего двух элементов H и C. |
|
|
|
|

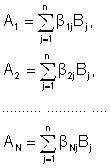 .
.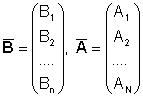 ,
,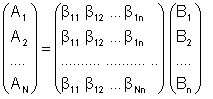 ,
,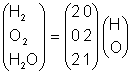 ,
,