| Темы | Предыдущий пункт | Следующий пункт | Литература |
|
|

Теория вероятностей |
|
13.1.7 Примеры вычисления вероятности событий
Пример 1. В первом ящике находится 10 бракованных и 15 годных деталей, которые тщательно перемешаны. Найти вероятность того, что a)Извлеченная деталь годная;b)Три извлеченные детали годные; c)Из трех извлеченных деталей две годные. Решение: В этой задаче имеем дело с конечной схемой равновозможных исходов. Поэтому возможно применение классического определения вероятности a)
Пример 2. Группа студентов из m человек садится в
пригородный электропоезд,
насчитывающий Задача на конечную схему
равновозможных исходов. Каждый студент
может выбрать один из n вагонов, поэтому число всех возможных
комбинаций равно
Замечание
При
больших n имеет место
асимптотическая формула Стирлинга
Пример 3. Из урны, содержащей М белых и N – M черных шаров, наудачу извлекается n шаров. Найти вероятность того, что среди выбранных n шаров окажется ровно m белых. Решение. В данной задаче
предполагается, что шары хорошо
перемешаны, все они одного радиуса,
отличаются только цветом и выбирающий
шаров не видит. В этом случае разумно
воспользоваться конечной схемой
равновозможных исходов и применить
классическое определение вероятности.
За элементарные события естественно
принять любые подмножества по n элементов выбранные из
множества N шаров. Число таких
подмножеств равно
Пример 4. Вычислить вероятность
приемки партии изделий, если объем
партии равен N,
число дефектных изделий в партии М. Для
контроля осуществляется выборка n
изделий из всей партии. , которая и
подвергается проверке на качество.
Партия бракуется, когда в выборке
обнаружено (с +1) или более дефектных
изделий. Естественно предположить,
что вероятности извлечения изделий из
партии равновероятны и извлеченное
изделие безошибочно классифицируется,
как годное или брак. Число дефектных
изделий х в
выборке может рассматриваться, как
случайная величина, принимающая
значения 0, 1, 2, …, n. Вероятность приемки партии
Р(А) будет равна вероятности того, что
случайная величина х примет значение
меньшее или равное с. Применяя схему
урн из предыдущей задачи, имеем На основании свойств вероятности,
вероятность приемки партии Например, вычислить
вероятность приемки партии, если N = 200, М = 26, n = 10, с = 1. По предыдущей
формуле находим Замечание.
Возможна следующая ситуация. Пусть N неизвестное число рыб в некотором
водоеме. Можно провести отлов М рыб,
пометить их и пустить обратно. Проведя
повторный отлов в количестве n рыб, в котором окажется
m помеченных рыб можно из
приближенного равенства
Пример 5. Из колоды в 52 карты
выбирается наугад одна. Какова
вероятность, что эта карта будет: 1)
червонной масти или король треф? 2)
червонной масти или один из королей? Решение. Введем
обозначения: А – событие, означающее,
что выбрана карта червонной масти; В –
событие, означающее что выбранная
карта – король; С – выбранная карта
король треф. Вероятности этих событий
согласно классического определения,
соответственно равны Так как
Пример 6. Некто выбирает наугад 6
клеток «Спортлото» (6 из 49). Найти
вероятность того, что он правильно
угадает из 6 выигравших номеров : A = {ровно
три}; В = {ровно четыре}; С = {ровно пять}; D = {все шесть}. Решение: Нетрудно
убедиться, что задача по структуре
полностью совпадает с задачей 3 (схемой
урн), если считать белые шары –
выигравшими номерами, а черные – не
выигравшими. Полагаем N
= 49, M = 6, m
последовательно равны: 3, 4, 5, 6. Применяя
формулу задачи 3, получим:
|
|
|
|
|
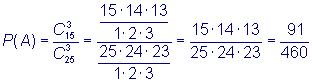 .
.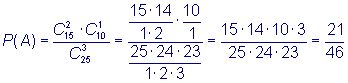 .
.