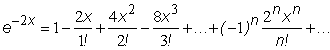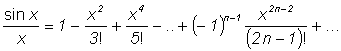| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Степенные ряды |
|
|
|
|
|
11.2.2. Формулы и ряды Тейлора и Маклорена. Разложение функций в степенные ряды.
|
||||||||||||||||||||||||
Если функция y = f(x) имеет производные в окрестности точки
x = x0 до (n+1) - го порядка включительно, то
существует точка
где Формула (1) называется формулой Тейлора функции y = f(x) для точки x0, Rn (x) - остаточным членом формулы Тейлора в форме Лагранжа. Многочлен называется многочленом Тейлора функции y = f(x). При x0 = 0 приходим к частному случаю формулы (1):
где Формула (2) называется формулой Маклорена функции y = f(x). Сформулируем условие разложимости функции в ряд Тейлора. Если функция f(x) дифференцируема в окрестности точки x0
любое число раз и в некоторой окрестности этой точки
При x0 = 0
Ряд (3) называется рядом Тейлора, а ряд (4) – рядом Маклорена. Приведем разложения в степенные ряды некоторых функций:
Для каждого случая в скобках указана область, в которой степенной ряд сходится к соответствующей функции.
Последний ряд, называемый биномиальным,
на концах интервала сходимости ведет себя по
- разному в зависимости от В общем случае разложение в степенные ряды основано на использовании рядов Тейлора или Маклорена. Но на практике степенные ряды многих функций можно найти формально, используя ряды (5 - 9). Например, при разложении в степенной ряд функции
Полученный ряд сходится при любых Аналогично
можно записать степенные ряды функций f (x) = e-2x и
Пример: Разложить в ряд Маклорена функцию: Разложим данную функцию на сумму простейших рациональных дробей:
Так как ряд
(10)
сходится при |
|
|