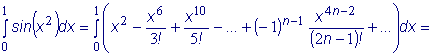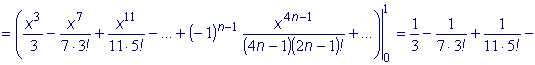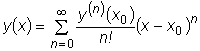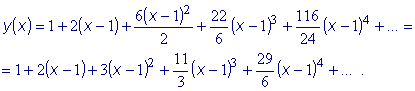| Темы | Предыдущий пункт | Следующая лекция | Литература | |
|
|
|

Степенные ряды |
|
|
|
|
|
11.2.3. Степенные ряды в приближенных вычислениях |
||||||
|
Вычисления значений функции |
||||||
|
Пусть дан степенной ряд функции y = f(x). Задача вычисления значения этой функции заключается в отыскании суммы ряда при заданном значении аргумента. Ограничиваясь определенным числом членов ряда, находим значение функции с точностью, которую можно устанавливать путем оценивания остатка числового ряда либо остаточного члена Rn(x) формул Тейлора или Маклорена.
Пример: Вычислить ln2 с точностью = 0,0001. Известно, что степенной ряд
при x = 1 сходится условно. Для того чтобы вычислить ln2 с помощью ряда (1) с точностью = 0,0001 необходимо взять не менее 10000 его членов. Поэтому воспользуемся рядом, который получается в результате вычисления степенных рядов функций ln(1+ x) и ln(1- x)
При
Для вычисления ln2 с заданной точностью необходимо найти
такое число n членов
частичной суммы Sn
при котором сумма остатка
Поскольку числа 2n + 3, 2n + 5 больше, чем 2n + 1 то, заменив их на 2n + 1 мы увеличим каждую дробь в формуле (3). Поэтому:
Путем подбора значений n находим, что для n = 3 rn<0.00015 и ln2 = 0,6931 | ||||||
|
Вычисление интегралов |
||||||
|
Так как степенные ряды сходятся равномерно на любом отрезке, лежащем внутри их интервалов сходимости, то с помощью разложений функций в степенные ряды можно находить неопределенные интегралы в виде степенных рядов и приближенно вычислять соответствующие определенные интегралы.
Пример:
Вычислить: В формуле (7) параграфа 7.2.2 заменим x на x2 , получим ряд:
Он сходится на всей числовой прямой,
поэтому его можно всюду почленно
интегрировать. Следовательно,
так как уже третий член полученного знакочередующегося ряда меньше | ||||||
|
Приближенное решение дифференциальных уравнений. |
||||||
В случае, когда точно проинтегрировать
дифференциальное уравнение с помощью
элементарных функций не
удается, его решение удобно искать в
виде степенного ряда, например, ряда
Тейлора или Маклорена. При решении задачи Коши
используется ряд Тейлора:
где
Пример: Найти пять первых членов разложения в степенной ряд решения дифференциального уравнения:
Из данного уравнения находим, что y'(1) = 1+1=2. Дифференцируем исходное уравнение: и т.д. Подставляя
найденные значения производных в ряд
(5), получаем
| ||||||
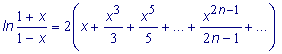
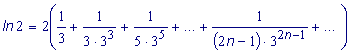 .
.
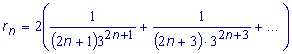
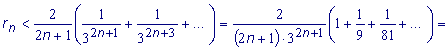
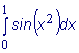 с точностью
с точностью